STATION REDUCTION AND STATION STATE PREDICTION

      In our project, we will use ANN?s to analyze a set of data taken from a specific test area to achieve a generalization. Neural networks in general have the capability of learning patterns and making conclusions about a certain situation through training and learning. In this case, in reducing the number of monitoring stations, we will train the neural network to recognize patterns in the occurrence of the high toxicity levels in different stations at different times. First we determine the variables that we need to be able to train the network. Upon careful study, we found that we only need a subset of the existing time-series data taken from the area under consideration in order for the network to make a reasonable conclusion about our problem. Table 1 gives the variables (along with their descriptions) that we found to be sufficient in order for the network to learn.

*Optional. While location information is not necessary, it is useful in making conclusions about the importance

of each station.

**Optional. While toxicity level is in itself enough, once the network has learned, the network can be used to 

predict an orbital approximation of the population of the organisms than can be found at a given station.

Having identified what we need, we go about preprocessing the data. Upon analysis of the variables we found that, with the exception of the toxicity level and the organism population, all data are uniform in distribution over the test space. We note however, that we must define a certain threshold value to identify the toxicity level measured at a given station as toxic. We also note that variations in the toxicity levels taken on certain time periods may not be uniform in the sense that it may noticeably rise or fall within such small time differences. In this case we will use a compression function on the data to ideally conform it to the overall distribution of the data. We also set up flag values to note toxic and non-toxic measurements. In the same sense, organism population differences taken within a specific time period may or may not center at a computed mean. In which case, centering will be performed on the population data set to speed up the learning process. Refer to MASTERS (1995) for an explanation of this method.

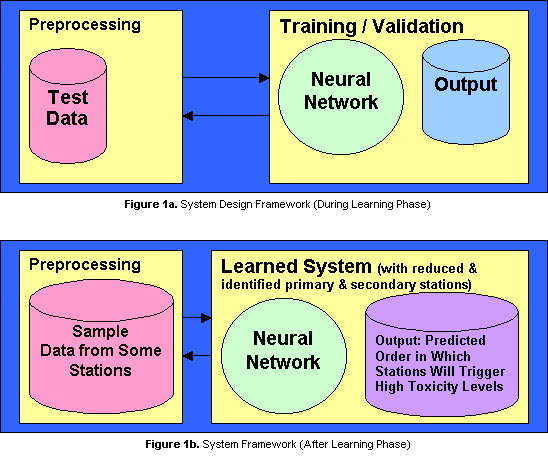
Having processed the data we feed them into the neural network continuously in random order until we an evaluation of the network reveals a consistent treatment of each station?s priority (i.e. it is able to identify the order by which each station will trigger toxic levels, at any time, when fed by data coming from selected stations only.) Training will stop once the network has achieved this consistency, in which case, the network will be able to assign priorities to the stations when given a specific scenario. Figure 1a shows the basic operational framework of the system during training and Figure 1b shows the system after its training. In summary, the framework is explained below.

During the training phase, the network is fed with a preprocessed subset of the time-series data. The goal is for the network to identify (1) patterns in the way each monitoring stations are triggered by high toxicity ratings as time progresses, (2) output some statistics for each individual station, (3)arrive at a generalization about the organism population as a function of the station numbers (or locations). Upon termination of the learning process, statistics outputted by the neural network, will be analyzed and will be used to remove redundant stations and hopefully identify gaps in the positioning of the stations over the area of coverage. Finally, the learned network can be used as a predictive tool, first for mapping the progression of red-tide from one station to another given a certain scenario, then second, for predicting the red-tide organism population that can appear at a specific station given initial data gathered by other stations.

In conclusion, artificial neural networks can be used modeling the progression of red-tide over an area of coverage given a minimal dimension of training data sets such as time, station sequence and location, toxicity, and population, is a feasible solution to the problem of reducing overhead maintenance cost of monitoring stations over a given area of coverage. Moreover, the said project can be applied used to solve similar reduction problems on other coverage areas just by re-training and on some areas, with minimal modifications to the system. 

Home